양자역학의 운동에는 translation, vibration, rotation이 있습니다. 여기서는 translation 운동 중 free particle과 particle in a box에 대해 계산해보겠습니다.
■ 자유 입자 (free particle)

■ 1차원 상자 속의 입자 (particle in a box)

이를 통해 몇 가지 특징을 알 수 있습니다.
1. 1차원 상자 속의 입자가 가지는 파동함수는 λ=2L/n 을 가지는 사인함수의 꼴을 띱니다.
2. |ψ|^2=0인 곳은 node라고 부르며, 그러한 node의 수는 n-1개입니다.
3. 고전역학에서는 구간 L에 대해, 입자가 발견될 확률은 각 지점에서 1/L로 동일합니다. 그러나 양자역학에서는 각 지점에서 입자가 발견될 확률이 λ=2L/n의 꼴을 갖는 사인함수의 형태를 갖습니다.
그런데 만약 n이 증가하면 |ψ|^2는 상수가 됩니다. 또 n이 증가하거나 E가 증가하면, 입자의 양자역학적 움직임은 고전역학적 움직임과 비슷해집니다. 이를 닐스 보어의 correspondence principle라고 합니다.
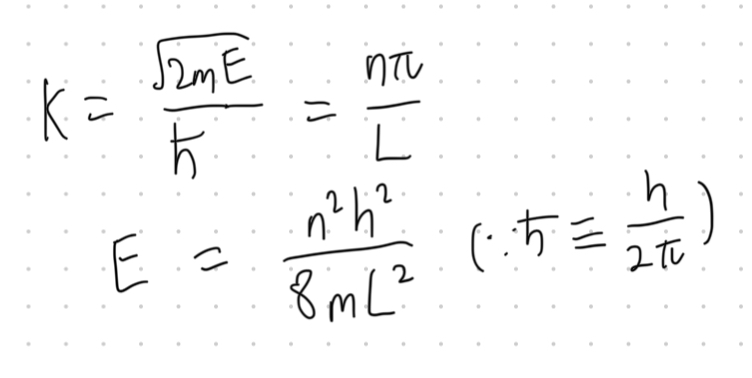
에너지는 위와 같이 계산됩니다. 그런데 이때 n은 정수이므로, 에너지가 양자화되어있다는 것을 알 수 있습니다.
여기서 Energy level diagram은 다음과 같습니다.

이때 중요한 것이 있습니다.
1. 가장 낮은 에너지가 0이 아닙니다. n의 최솟값이 1이기 때문입니다.
2. 에너지는 n^2에 비례합니다. 이에 따라 ΔE=(En+1)-(En)=h^2/8mL^2 (2n+1)에서 ΔE가 n에 비례한다는 것을 알 수 있습니다.
3. 에너지는 L^2와 1/m에 비례합니다. 마찬가지로 ΔE도 L^2와 1/m에 비례합니다.
그런데 이때 ΔE가 작으면 파장 λ는 커집니다. 이에 따라 particle in a box 문제는 다음과 같이 응용됩니다.
1. 양자점 현상(Quantum Dots)
양자점은 전자를 작은 구 안에 가둬두는 형태를 띱니다. 일종의 particle in a box 문제입니다. 이때 구의 크기가 커지면 n이 커지고 ΔE가 커지며 파장 λ가 더 높은 빛을 흡수하게 되며, 따라서 우리의 눈에는 파장 λ가 더 낮은 빛이 보이게 됩니다.
이를 양자갇힘효과(Quantum Confinement Effect)라고 합니다.
2. 공액계 분자(conjugated molecule)
공액계 분자는 2중결합과 1중결합이 반복되어 나타나는 분자로, 이때 π결합이 서로 이어져 하나의 선으로 이어집니다.
이때 만약 π결합이 매우 길어지게 되면, particle in a box 문제에서 구간 L이 길어지는 효과를 냅니다. L이 증가하면 ΔE가 증가하고, 파장 λ가 더 높은 빛을 흡수하게 되며, 따라서 우리의 눈에는 파장 λ가 더 낮은 빛이 보이게 됩니다.
■ 2차원 상자 속의 입자 (particle in a 2D box)

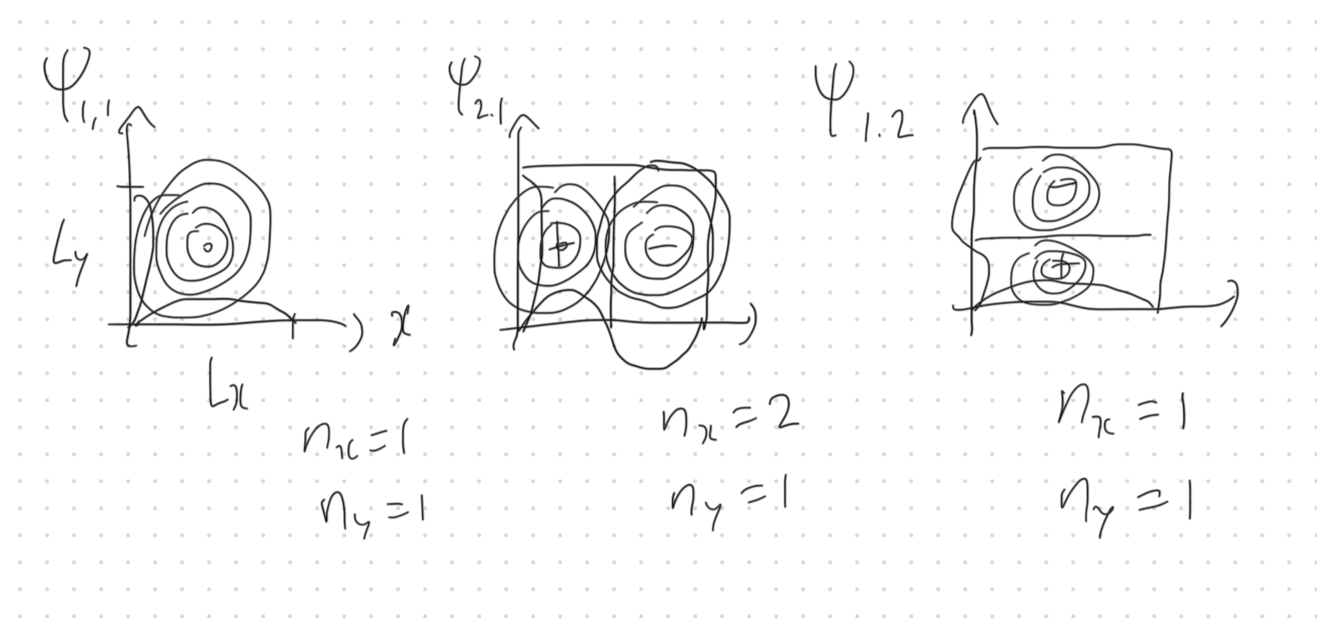
2차원 상자 속의 입자 문제는 변수분리법으로 해결합니다.
이때 확률분포는 위와 같습니다.
그런데 만약 Lx와 Ly가 같은 값을 갖는다면, 축퇴(degeneracy) 현상이 발생합니다. 서로 다른 파동함수가 동일한 에너지를 갖게 되는 현상입니다.
축퇴 현상이 깨지게 되면, symmetric은 broken되고, degeneracy는 lifted됩니다.
'과학과 수학' 카테고리의 다른 글
| [양자역학] 3. 슈뢰딩거 방정식 (2) - 진동 운동 (0) | 2024.06.13 |
|---|---|
| [고전역학] 뉴턴역학의 기초와 보존법칙의 증명 (2) | 2024.05.31 |
| [양자역학] 2. 양자역학의 공리 (4) - 원자모형의 기본 (2) | 2024.04.25 |
| [양자역학] 2. 양자역학의 공리 (3) - 중첩과 불확정성 원리 (0) | 2024.04.25 |
| [양자역학] 2. 양자역학의 공리 (2) - 연산자 (0) | 2024.04.21 |