728x90
■ 슈뢰딩거 방정식
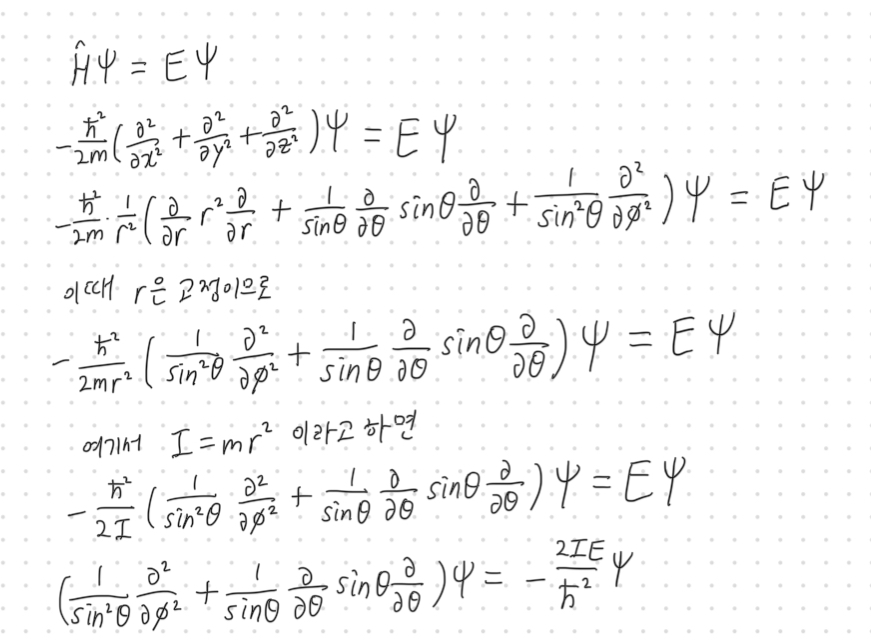


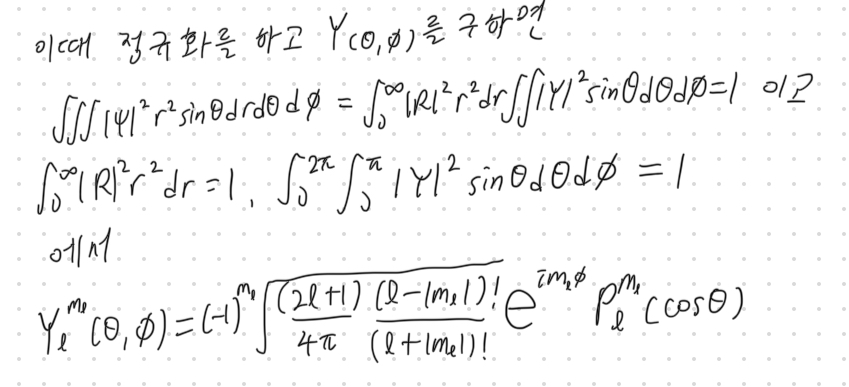
2차원 회전 운동에 대한 슈뢰딩거 방정식을 만들면 r은 고정이므로 θ와 φ에 대한 함수가 나옵니다.
그렇게 변수분리법으로 정리하고 나면 φ에 대한 함수는 2차원 회전 운동 때와 같게 되고, θ에 대한 함수는 버금 르장드르 다항식을 사용할 수 있는 미분방정식이 나오게 됩니다. 그리고 이를 곱하고 정규화하면 최종적인 파동함수가 나오게 됩니다.

여기서 2IE/ħ^2 = l(l+1)이 성립합니다.
여기서 l은 방위양자수(azimuthal quantum number), 각양자수, 부양자수, 궤도양자수 등으로 불립니다.
■ 에너지와 각운동량

■ 알 수 있은 사실
여기서 알 수 있는 사실이 있습니다.
1. 에너지는 l이랑만 연결되어 있으며 ml과는 상관 없습니다.
2. degeneracy는 2l+1입니다.
3. Zero point energy(영점 에너지)는 없으며, 에너지가 0일 수 있습니다.
'과학과 수학' 카테고리의 다른 글
| [양자역학] 3. 슈뢰딩거 방정식 (5) - 수소 원자 (0) | 2024.06.20 |
|---|---|
| [고전역학] 라그랑주 역학과 해밀토니안 역학 (0) | 2024.06.18 |
| [양자역학] 3. 슈뢰딩거 방정식 (3) - 2차원 회전 운동 (2) | 2024.06.13 |
| [양자역학] 3. 슈뢰딩거 방정식 (2) - 진동 운동 (0) | 2024.06.13 |
| [고전역학] 뉴턴역학의 기초와 보존법칙의 증명 (2) | 2024.05.31 |